熵、相对熵与互信息
熵
定义：一个离散型随机变量 $X$ 的熵 $H(X)$ 定义为： $$ H(X)=-\sum_{x \in X}p(x) \log p(x) $$ 注释：$X$ 的熵又可以理解为随机变量 $\log \frac{1}{p(X)}$ 的期望值
引理
- $H(X) \geq 0$
- $H_b(X)=(\log_ba)H_a(X)$
二元熵： $$ H(X)= -p\log p-(1-p)\log (1-p) \rightarrow H(p) $$ $H(p)$ 为上凸函数，在 $p= \frac{1}{2}$ 时取得最大值 1
联合熵与条件熵
定义：对于服从联合分布为 $p(x,y)$ 的一对离散随机变量 $(x,y)$ ，其联合熵 $H(X,Y)$ 定义为： $$ \begin{aligned} H(X,Y)=&-\sum_{x\in X} \sum_{y \in Y}p(x,y)\log p(x,y)\\ =&-E \log p(X,Y) \end{aligned} $$ 定义：条件熵 $H(Y|X)$ 定义为： $$ \begin{aligned} H(Y|X)=&\sum_{x \in X}p(x)H(Y|X=x)\\ =&-\sum_{x \in X}p(x)\sum_{y \in Y}p(y|x)\log p(y|x)\\ =&-\sum_{x \in X} \sum_{y \in Y}p(x,y)\log p(y|x)\\ =&-E \log p(Y|X) \end{aligned} $$ 定理：链式法则 $$ H(X,Y)=H(X)+H(Y|X) $$ 证明： $$ \begin{aligned} H(X,Y)=&-\sum_{x\in X} \sum_{y \in Y}p(x,y)\log p(x,y)\\ =&-\sum_{x\in X} \sum_{y \in Y}p(x,y)\log p(x) p(y|x)\\ =&-\sum_{x\in X} \sum_{y \in Y}p(x,y)\log p(x) -\sum_{x\in X} \sum_{y \in Y}p(x,y)\log p(y|x)\\ =&-\sum_{x \in X}p(x) \log p(x)-\sum_{x\in X} \sum_{y \in Y}p(x,y)\log p(y|x)\\ =&H(X)-H(Y|X) \end{aligned} $$ 等价于： $$ \log p(X,Y)=\log p(X)+\log p(Y|X) $$ 推论： $$ H(X,Y|Z)=H(X|Z)+H(Y|X,Z) $$
相对熵和互信息
相对熵（relative entropy） 是两个随机分布之间距离的度量。相对熵 $D(p||q)$ 度量当真实分布为 $p$ 而假定分布为 $q$ 时的无效性。
定义：两个概率密度函数为 $p(x)$ 和 $q(x)$ 之间的相对熵或 $\text{Kullback-Leibler}$ 距离定义为 $$ \begin{aligned} D(p||q)=&\sum_{x \in X}p(x)\log \frac{p(x)}{q(x)}\\ =&E_p \log \frac{p(x)}{q(x)} \end{aligned} $$ 互信息（mutual information） 是一个随机变量包含另一个随机变量信息量的度量。互信息也是给定另一个随机变量知识的条件下，原随机变量不确定度的缩减量。
定义：考虑两个随机变量 $X$ 和 $Y$，它们的联合概率密度函数为 $p(x,y)$，其边际概率密度函数为 $p(x)$ 和 $p(y)$。互信息 $I(X;Y)$ 为联合概率分布 $p(x,y)$ 和乘积分布 $p(x)p(y)$ 之间的相对熵 $$ \begin{aligned} I(X;Y)=&\sum_{x \in X,y \in Y}p(x,y) \log \frac{p(x,y)}{p(x)p(y)}\\ =& D(p(x,y)||p(x)p(y)) \end{aligned} $$ 注：一般情况下 $D(p||q) \neq D(q||p)$
熵和互信息的关系
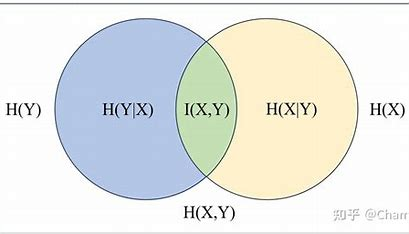
互信息 $I(X;Y)$ 可重写为： $$ \begin{aligned} I(X;Y)=&\sum_{x \in X,y \in Y}p(x,y) \log \frac{p(x,y)}{p(x)p(y)}\\ =& \sum_{x \in X,y \in Y}p(x,y) \log \frac{p(x|y)}{p(x)}\\ =& \sum_{x \in X,y \in Y}p(x,y) \log p(x|y)-\sum_{x \in X,y \in Y}p(x,y) \log p(x)\\ =& \sum_{x \in X,y \in Y}p(x,y) \log p(x|y)-\sum_{x \in X}p(x) \log p(x)\\ =& H(X)-H(X|Y) \end{aligned} $$ 由此可表明互信息 $I(X;Y)$ 是给定 $Y$ 的情况下 $X$ 的不确定度的缩减量。
由对称性，可得： $$ I(X;Y)=H(Y)-H(Y|X) $$ 由 $H(X,Y)=H(X)+H(Y|X)$ 可得： $$ I(X;Y)=H(X)+H(Y)-H(X,Y) $$ 最后注意到： $$ I(X;X)=H(X)-H(X|X)=H(X) $$ 因此，随机变量和自身的互信息为该随机变量的熵，因此将熵称为自信息（self-information）
定理：互信息与熵的关系 $$ \begin{aligned} I(X;Y)=&H(X)-H(X|Y)\\ I(X;Y)=&H(Y)-H(Y|X)\\ I(X;Y)=&H(X)+H(Y)-H(X;Y)\\ I(X;Y)=&I(Y;X)\\ I(X;X)=&H(X)\\ \end{aligned} $$ Venn 图：互信息和熵的关系可由文氏图给出
熵、相对熵与互信息的链式法则
定理（熵的链式法则）： $$ H(X_1,X_2, \cdots ,X_n)=\sum_{i=1}^{n}H(X_i|X_{i-1},\cdots,X_1) $$ 证明： $$ \begin{aligned} H(X_1,X_2)=&H(X_1)+H(X_2|X_1)\\ H(X_1,X_2,X_3)=&H(X_1)+H(X_2,X_3|X_1)\\ =&H(X_1)+H(X_2|X_1)+H(X_3|X_2,X_1)\\ \cdots\\ H(X_1,X_2, \cdots ,X_n)=&\sum_{i=1}^{n}H(X_i|X_{i-1},\cdots,X_1) \end{aligned} $$ 定义（条件互信息）：随机变量 $X$ 和 $Y$ 在给定随机变量 $Z$ 时的条件互信息定义为 $$ \begin{aligned} I(X;Y|Z)=&H(X|Z)-H(X|Y,Z)\\ =&E_{p(x,y,z)} \log \frac{p(X,Y|Z)}{p(X|Z)p(Y|Z)} \end{aligned} $$ 定理（互信息的链式法则）： $$ I(X_1,X_2,\cdots ,X_n;Y)=\sum^n_{i=1}I(X_i;Y|X_{i-1},X_{i-2},\cdots ,X_1) $$ 证明： $$ \begin{aligned} I(X_1,X_2,\cdots ,X_n;Y)=&H(X_1,X_2,\cdots ,X_n)-H(X_1,X_2,\cdots ,X_n|Y)\\ =& \sum_{i=1}^n H(X_i|X_{i-1},\cdots,X_1)-\sum_{i=1}^n H(X_i|X_{i-1},\cdots,X_1,Y)\\ =& \sum_{i=1}^n I(X_i;Y|X_{i-1},\cdots,X_1) \end{aligned} $$
Jensen 不等式及其结果
定义（下凸函数）：若对于任意的 $x_1,x_2 \in (a,b)$ 及 $0 \leq \lambda \leq 1$，满足 $$ f(\lambda x_1+(1-\lambda)x_2) \leq \lambda f(x_1)+(1-\lambda)f(x_2) $$ 则称函数 $f(x)$ 在区间 $(a,b)$ 上是严格下凸的。
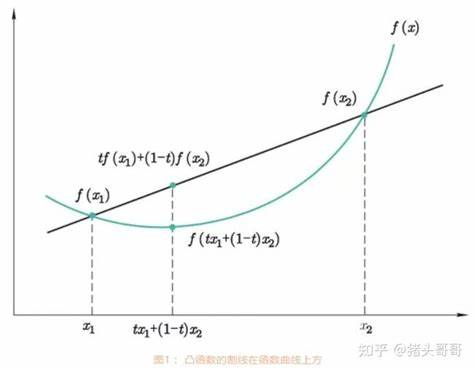
定理：如果函数 $f$ 在某个区间存在非负的二阶导数，则 $f$ 为该区间的凸函数。
定理（Jessen 不等式）：若给定一个下凸函数 $f$ 和一个随机变量 $X$ ，则 $$ Ef(X)\geq f(EX) $$ 证明：利用数学归纳法进行证明，对于一个两点分布，我们有 $$ p_1f(x_1)+p_2f(x_2)\geq f(p_1x_1+p_2x_2) $$ 设分布点个数为 $k-1$ 的时候定理成立，此时记 $p_i’=\frac{p_i}{1-p_k}(i=1,2,\dots k-1)$，则有 $$ \begin{aligned} \sum_{i=1}^k p_if(x_1) =& p_kf(x_k)+(1-p_k)\sum_{i=1}^{k-1}p_i’f(x_i)\\ \geq & p_kf(x_k)+(1-p_k)f(\sum_{i=1}^{k-1}p_i’x_i)\\ \geq & f(p_kx_k+(1-p_k)\sum_{i=1}^{k-1}p_i’x_i)\\ \geq & f(\sum_{i=1}^k p_ix_i) \end{aligned} $$ 定理（信息不等式）：设 $p(x)$，$q(x)$ 为两个概率密度函数，则 $$ D(p(x)||q(x)) \geq 0 $$ 当且仅当对任意的 $x$ ，$p(x)=q(x)$ 时等号成立。
证明： $$ \begin{aligned} -D(p||q)=&-\sum_{x \in X}p(x)\log \frac{p(x)}{q(x)}\\ =&\sum_{x \in X}p(x)\log \frac{q(x)}{p(x)}\\ \leq & \log \sum_{x \in X} p(x)\frac{q(x)}{p(x)}\\ =& \log \sum_{x \in X} q(x)\\ =& \log 1\\ =& 0 \end{aligned} $$ 当且仅当 $\frac{q(x)}{p(x)}=c$ 时等号成立，$\sum_{x \in X}c p(x)=1 \rightarrow c=1 \rightarrow p(x)=q(x)$
推论（互信息的非负性）：对于任意两个随机变量 $X$，$Y$， $$ I(X;Y) \geq 0 $$ 证明：$I(X;Y)=D(p(x,y)||p(x)p(y)) \geq 0$，当且仅当 $p(x,y)=p(x)p(y)$ ，即 $X$ 和 $Y$ 相互独立时取等号。
定理：$H(X) \leq \log |\chi|$，其中 $\chi$ 为 $X$ 的字母表 $\chi$ 的元素个数，当且仅当 $X$ 服从 $\chi$ 上的均匀分布时，等号成立。
证明：设 $u(x)=\frac{1}{|\chi|}$ ，$p(x)$ 是随机变量 $X$ 的概率密度函数，有 $$ D(p||u)=\sum p(x)\log \frac{p(x)}{u(x)}= \log |\chi | -H(X) \geq 0 $$ 定理（条件作用使熵减小）： $$ H(X|Y) \leq H(X) $$ 当 $X$ 和 $Y$ 相互独立时，等号成立。
定理（熵的独立界）： $$ H(X_1,X_2, \cdots ,X_n) \leq \sum_{i=1}^n H(X_i) $$ 当且仅当 $X_i$ 相互独立时等号成立。
证明：根据熵的链式法则 $$ \begin{aligned} H(X_1,X_2, \cdots ,X_n) = & \sum_{i=1}^n H(X_i|X_{i-1},\cdots,X_1)\\ \leq & \sum_{i=1}^n H(X_i) \end{aligned} $$
数据处理不等式
定义（马尔可夫链）： 如果 $Z$ 的条件分布仅依赖于 $Y$ 的分布，而与 $X$ 是条件独立的，则称随机变量 $X,Y,Z$ 依序构成马尔可夫（Markov）链，记作：$X \rightarrow Y \rightarrow Z$。若 $X,Y,Z$ 的联合概率密度函数可写为 $$ p(x,y,z)=p(x)p(y|x)p(z|y) $$ 则 $X,Y,Z$ 构成马尔可夫链 $X \rightarrow Y \rightarrow Z$。
一些简单结果如下：
- $X \rightarrow Y \rightarrow Z$，当且仅当在给定 $Y$ 时，$X$ 和 $Z$ 是条件独立的：
$$ p(x,z|y)=\frac{p(x,y,z)}{p(y)}=\frac{p(x)p(y|x)p(z|y)}{p(y)}=\frac{p(x,y)p(z|y)}{p(y)}=p(x|y)p(z|y) $$
- $X \rightarrow Y \rightarrow Z$ 蕴含 $Z \rightarrow Y \rightarrow X$。有时可记为 $X \leftrightarrow Y \leftrightarrow Z$。
- 若 $Z = f(Y)$ ，则 $X \rightarrow Y \rightarrow Z$。
定理（数据处理不等式）： 若 $X \rightarrow Y \rightarrow Z$ ，则有 $I(X;Y) \geq I(X;Z)$。
证明： 使用 Double Counting ，将 $I(X;Y,Z)$ 以两种方式展开 $$ \begin{aligned} I(X;Y,Z)=&I(X;Z)+I(X;Y|Z)\\ =&I(X;Y)+I(X;Z|Y) \end{aligned} $$ 由于在给定 $Y$ 的情况下，$X$ 和 $Z$ 是条件独立的，因此 $I(X;Z|Y)=0$，由互信息的性质，$I(X;Y|Z) \geq 0$ ，因此我们可以推出： $$ I(X;Y) \geq I(X;Z) $$ 当且仅当 $I(X;Y|Z) = 0$ 时，也就是 $X \rightarrow Z \rightarrow Y$ 构成马尔可夫链时，等号成立。类似的，根据 $Z \rightarrow Y \rightarrow X$ 可得 $I(Z;Y) \geq I(Z;X)$
推论： 如果 $Z=g(Y)$ ，则 $I(X;Y) \geq I(X;g(Y))$。
证明： $X \rightarrow Y \rightarrow g(Y)$ 构成马尔可夫链。
推论： 如果 $X \rightarrow Y \rightarrow Z$ ，则 $I(X;Y|Z) \leq I(X;Y)$
证明： 根据上面 Double Counting 的两式可得。
Fano 不等式
我们想通过随机变量 $Y$ 推测 $\hat{X}$ ，有 $g(Y)=\hat{X}$ ，其中 $\hat{X}$ 是对 $X$ 的估计，注意到 $X \rightarrow Y \rightarrow \hat{X}$ 构成马尔可夫链。我们定义估计误差概率为 $$ P_e = \text{Pr}\{\hat{X} \neq X\} $$ 定理（Fano 不等式）： 对任何满足 $X \rightarrow Y \rightarrow \hat{X}$ 的估计量 $\hat{X}$ ，有 $$ H(P_e)+P_e\log |\chi| \geq H(X|\hat{X}) \geq H(X|Y) $$ 上面的不等式可以减弱为： $$ 1+P_e \log |\chi| \geq H(X|Y) \\ P_e \geq \frac{H(X|Y)-1}{\log |\chi|} $$ 注释： 当 $P_e = 0$ 时，可推出 $H(X|Y)=0$ ，直观理解，当错误概率为 0 时，$X=\hat{X}=g(Y)$
证明： 首先定义一个误差随机变量 $$ E = \begin{cases} 1& \hat{X} \neq X \\ 0& \hat{X} = X \end{cases} $$ 利用 Double Counting 将 $H(E,X|\hat{X})$ 展开 $$ \begin{aligned} H(E,X|\hat{X})=& H(X|\hat{X})+H(E|X,\hat{X})\\ =& H(E|\hat{X})+H(X|E,\hat{X}) \end{aligned} $$ 易得 $H(E|X,\hat{X})=0$ ，由条件作用 $H(E|\hat{X}) \leq H(P_e)$ ，对于 $H(X|E,\hat{X})$，有 $$ H(X|E,\hat{X})=Pr(E=0)H(X|E=0,\hat{X})+Pr(E=1)H(X|E=1,\hat{X})\leq 0+P_e \log |\chi| $$ 可得： $$ P_e \log |\chi|+H(P_e) \geq H(X|\hat{X}) $$ 又由于 $X \rightarrow Y \rightarrow \hat{X}$ 构成马尔可夫链，故 $I(X;Y)\geq I(X;\hat{X})$ ，从而 $H(X)-H(X|Y) \geq H(X)-H(X|\hat{X})$，从而 $H(X|Y) \leq H(X|\hat{X})$，于是有： $$ P_e \log |\chi|+H(P_e) \geq H(X|\hat{X})\geq H(X|Y) $$ 若估计量 $g(Y)$ 在集合 $\chi$ 中取值，那么可以将 $\log |\chi|$ 替换为 $\log (|\chi|-1)$（因为$\hat{X}$ 已经猜错了，所以减去1），有 $$ P_e \geq \frac{H(X|Y)-1}{\log (|\chi|-1)} $$
渐进均分性
在信息论中，与大数定律类似的是渐进均分性（AEP），它是弱大数定律的直接结果。大数定律表明，对于独立同分布（i.i.d.）的随机变量，当 $n$ 很大的时候，$\frac{1}{n}\sum_{i=1}^nX_i$ 近似于期望值 $EX$。渐进均分性表明，$\frac{1}{n} \log \frac{1}{P(X_1,X_2,\cdots,X_n)}$ 近似于熵 $H$ ，当 $n \rightarrow +\infty$ 时，$p(X_1,X_2,\cdots,X_n)$ 近似于 $2^{-nH}$。
马尔可夫不等式与切比雪夫不等式
定理（马尔可夫不等式）： 对任意非负随机变量 $X$ 以及任意的 $t>0$ ，有 $$ Pr\{X > t\} \leq \frac{EX}{t} $$ 证明： 设 $f(x)$ 是 $X$ 的概率密度函数，则 $EX = \int _0^\infty xf(x)dx$，对于 $\forall t>0$，有 $$ EX = \int _0^t xf(x)dx+ \int _t^\infty xf(x)dx $$ 在区间 $(t,+\infty)$ 上，有 $$ \int _t^\infty xf(x)dx \geq \int _t^\infty tf(x)dx=t \int _t^\infty f(x)dx=tPr[X>t] $$ 又由于 $\int _0^t xf(x)dx \geq 0$，则 $$ EX \geq tPr[X>t]\\ Pr[X > t] \leq \frac{EX}{t} $$ 定理（切比雪夫不等式）： 设随机变量 $Y$ 的均值和方差为 $\mu$ 和 $\sigma^2$ ，对$\forall \varepsilon>0$有 $$ Pr[|Y- \mu|>\varepsilon] \leq \frac{\sigma^2}{\varepsilon^2} $$ 证明： 令 $X = (Y-\mu)^2$，由马尔可夫不等式 $$ Pr[(Y-\mu)^2>\varepsilon^2]\leq \frac{E(Y-\mu)^2}{\varepsilon^2} $$ 由于 $E(Y-\mu)^2=\sigma^2$ 则切比雪夫不等式得证。
定理（弱大数定律）： 设 $Z_1,Z_2, \cdots , Z_n$ 为 i.i.d. 随机变量序列，其均值和方差为 $\mu$ 和 $\sigma^2$，令 $\overline{Z_n}=\frac{1}{n} \sum_{i=1}^nZ_i$ 为样本均值，则 $$ Pr[|\overline{Z_n}-\mu|>\varepsilon] \leq \frac{\sigma^2}{n \varepsilon^2} $$ 证明： 只需证明 $E(\overline{Z_n}-\mu)^2=\frac{\sigma^2}{n}$ $$ \begin{aligned} E(\overline{Z_n}-\mu)^2=&E(\frac{1}{n} \sum_{i=1}^nZ_i-\mu)^2\\ =& \frac{1}{n^2}E(\sum_{i=1}^nZ_i-n\mu)^2\\ =& \frac{1}{n^2}Var(\sum_{i=1}^nZ_i)\\ =& \frac{1}{n^2}\sum_{i=1}^nVar(Z_i)\\ =& \frac{1}{n^2}n\sigma^2\\ =&\frac{\sigma^2}{n} \end{aligned} $$
渐进均分性定理
定义（随机变量的收敛）： 给定一个随机变量序列 $X_1,X_2,\cdots$。有三种情形
- 如果对任意的 $\varepsilon >0$，$Pr[|X_n-X|>\varepsilon]\rightarrow 0$，称为依概率收敛。
- 如果 $E(X_n-X)^2 \rightarrow 0$ ，称为均方收敛。
- 如果 $Pr[\lim_{n\rightarrow \infty}X_n=X]=1$，称为以概率 1 收敛。
定理（AEP）： 若 $X_1,X_2,\cdots ,X_n$ 为 $i.i.d.\sim p(x)$，则 $$ -\frac{1}{n}\log p(X_1,X_2,\cdots,X_n) \rightarrow H(X) $$ 依概率收敛。
证明： 独立随机变量的函数依然是独立随机变量，又由于 $X_i$ 是 $i.i.d.$ ，从而 $\log X_i$ 也是 $i.i.d.$ ，由弱大数定律 $$ \begin{aligned} Pr[|\overline{Z_n}-\mu|>\varepsilon] \leq \frac{\sigma^2}{n \varepsilon^2}\\ -\overline{\log p(X_n)}-\frac{1}{n}\log p(X_1,X_2,\cdots,X_n)=&-\frac{1}{n} \sum_i \log p(X_i)\\ \rightarrow & -E\log p(X)\\ =& H(X) \end{aligned} $$ 定义（典型集）： 关于 $p(x)$ 的典型集 $A_{\varepsilon}^{(n)}$ 是序列 $(x_1,x_2, \cdots,x_n) \in \chi^n$ 的集合，且满足性质： $$ 2^{-n(H(X)+\varepsilon)} \leq p(x_1,x_2, \cdots,x_n) \leq 2^{-n(H(X)-\varepsilon)} $$ 典型集 $A_{\varepsilon}^{(n)}$ 的性质：
- 如果 $(x_1,x_2, \cdots,x_n) \in A_{\varepsilon}^{(n)}$ ，则 $H(X)- \varepsilon \leq -\frac{1}{n} \log p(x_1,x_2, \cdots,x_n) \leq H(X)+\varepsilon$
- 当 $n$ 充分大时，$Pr[A_{\varepsilon}^{(n)}]>1-\varepsilon$。
- $|A_{\varepsilon}^{(n)}| \leq 2^{n(H(X)+\varepsilon)}$
- 当 $n$ 充分大时，$|A_{\varepsilon}^{(n)}| \geq (1-\varepsilon)2^{n(H(X)-\varepsilon)}$
证明（性质 3）: 由典型集的定义 $$ \begin{aligned} 1=& \sum_{x \in \mathcal{X}^n}p(x)\\ \geq & \sum_{x \in A_{\varepsilon}^{(n)}}p(x)\\ \geq & \sum_{x \in A_{\varepsilon}^{(n)}}2^{-n(H(X)+\varepsilon)}\\ =& 2^{-n(H(X)+\varepsilon)}|A_{\varepsilon}^{(n)}| \end{aligned} $$ 证明（性质 4）： 当 $n$ 充分大的时候，由性质 2 得 $$ \begin{aligned} 1- \varepsilon <& Pr[A_{\varepsilon}^{(n)}]\\ \leq & \sum_{x \in A_{\varepsilon}^{(n)}}2^{-n(H(X)-\varepsilon)}\\ =&2^{-n(H(X)-\varepsilon)}|A_{\varepsilon}^{(n)}| \end{aligned} $$ 定理： 设 $X^n$ 是服从 $p(x)$ 的 $i.i.d.$ 序列，则存在一个编码将长度为 $n$ 的序列 $x^n$ 映射为比特串，且为一一映射，对于充分大的 $n$ ，有 $$ E(\frac{1}{n}l(X^n)) \leq H(X)+\varepsilon $$ 也就是说这个一个长度的原始序列最少可以用 $H(X)$ 长度的比特串来编码，用 $nH(X)$ 比特可以表示序列 $X^n$
数据压缩
基础概念
定义： 关于随机变量 $X$ 的信源编码 $C$ 是从 $X$ 的取值空间 $\mathcal{X}$ 到 $\mathcal{D}^*$ 的一个映射，其中 $\mathcal{D}^*$ 表示 $D$ 元字母表 $\mathcal{D}$ 上有限长度的字符串所构成的集合。用 $C(x)$ 表示 $x$ 的码字，用 $l(x)$ 表示 $C(x)$ 的长度。
定义： 设随机变量 $X$ 的概率密度函数为 $p(x)$ ，定义信源编码 $C(x)$ 的期望长度 $L(C)$ 为 $$ L(C)=\sum_{x \in \mathcal{X}}p(x)l(x) $$ 定义： 如果编码将 $X$ 取值空间中的每一个元素映射成 $\mathcal{D}^*$ 中不同的字符串，即 $$ x \neq x’ \Rightarrow C(x) \neq C(x’) $$ 则称这个编码是非奇异的（nonsigular）。
定义： 编码 $C$ 的扩展 $C^*$ 是从 $\mathcal{X}$ 上的有限长字符串到 $\mathcal{D}$ 上的有限长字符串的映射，定义为 $$ C(x_1,\cdots,x_n)=C(x_1)C(x_2)\cdots C(x_n) $$ 其中 $C(x_1)C(x_2)\cdots C(x_n)$ 表示相应码字的串联。
定义： 如果一个编码的拓展编码是非奇异的，那么称该编码是惟一可译的。
定义： 若码中无任何码字是其他码字的前缀，则称该编码为前缀码或即时码。
| X | 奇异的 | 非奇异，但不惟一可译 | 惟一可译，但不即时 | 即时的 |
|---|---|---|---|---|
| 1 | 0 | 0 | 10 | 0 |
| 2 | 0 | 010 | 00 | 10 |
| 3 | 0 | 01 | 11 | 110 |
| 4 | 0 | 10 | 110 | 111 |
Kraft 不等式
定理（Kraft 不等式）： 对于 {0,1} 上的即时码（前缀码），码字长度 $l_1,\cdots,l_m$ 必定满足不等式 $$ \sum_i 2^{-l_i} \leq 1 $$ 反之，若给定一组码字长度满足上式，则存在相应长度的即时码。
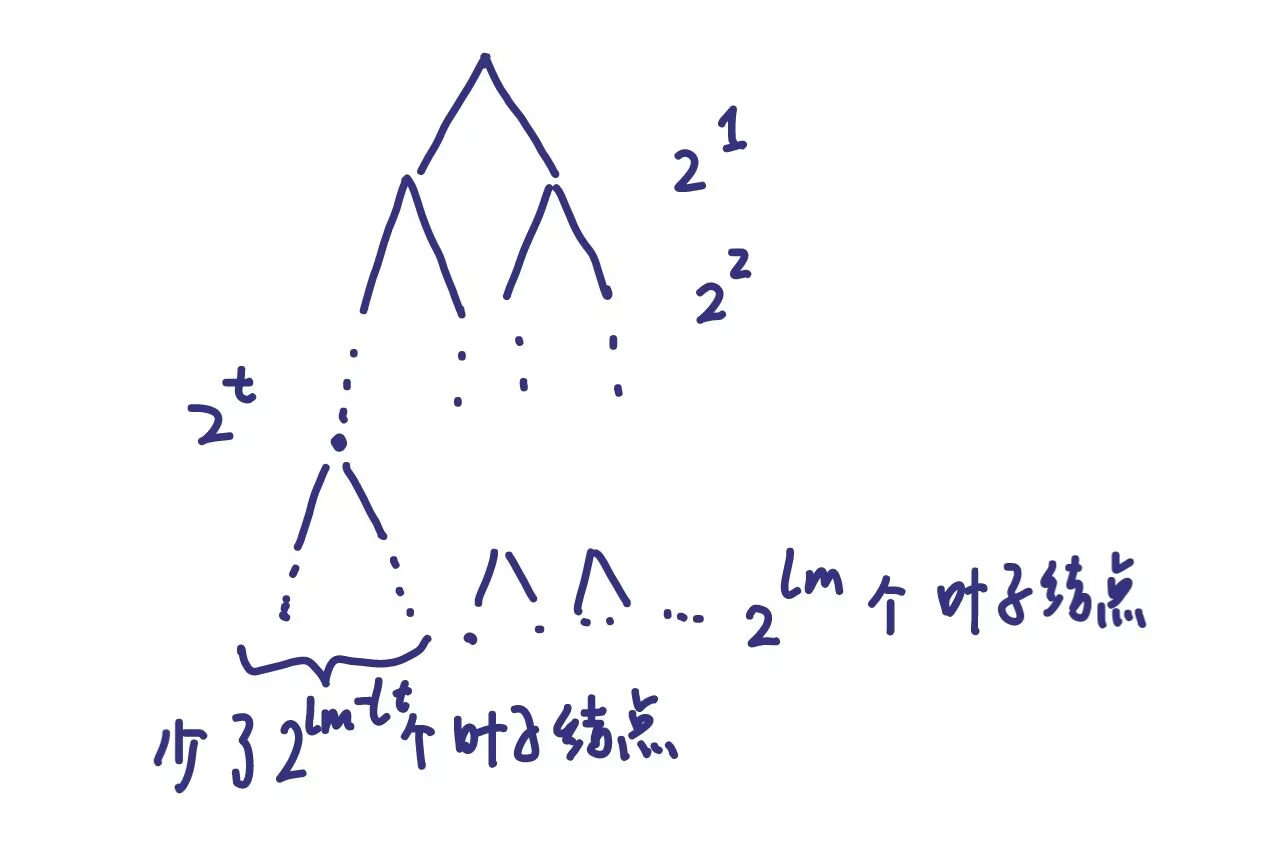
证明： 构造一个高度为 $l_m$ 的二叉树，完全二叉树的总叶子结点数为 $2^{l_m}$ ，码字长度为 $l_t$ 的码会消耗 $2^{l_m-l_t}$ 的叶子结点，我们有消耗的叶子结点不会多于总的叶子结点，因此有 $$ 2^{l_m-l_1}+2^{l_m-l_2}+\cdots + 2^{l_m-l_m} \leq 2^{l_m} \Rightarrow 2^{-l_1}+2^{-l_2}+\cdots2^{-l_m} \leq 1 $$
最优码
我们想找到一种最优的编码方案，在满足 Kraft 不等式的前提下，使平均码长最小，也就是 $$ \min \{L=\sum p_il_i\}\\ \sum 2^{-l_i} \leq 1 $$ 定理： 随机变量 $X$ 的任一二元即时码的期望长度必定大于等于熵 $H(X)$ ，即 $$ L \geq H(X) $$ 当且仅当 $2^{-l_i}=p_i$ 时等号成立。
证明： 将期望长度与熵作差，写成如下形式 $$ \begin{aligned} L-H(X)=&\sum_i p_il_i - \sum_i p_i \log \frac{1}{p_i}\\ =&-\sum_i p_i\log 2^{-l_i} + \sum_i p_i \log p_i \end{aligned} $$ 设 $S = \sum_i 2^{-l_i}$ ，$q_i = 2^{-l_i}/S$，有 $$ \begin{aligned} L-H(X)=&-\sum_i p_i \log(Sq_i) + \sum_i p_i \log p_i\\ =& \sum_i p_i \log p_i -\sum_i p_i \log q_i -\sum_i p_i \log S\\ =& \sum_i p_i \log \frac{p_i}{q_i} -\log S\\ =& D(p||q) - \log S \end{aligned} $$ 根据相对熵的非负性可知 $D(p||q) \geq 0$ ，由 Kraft 定理可知 $S \leq 1 \Rightarrow -\log S \geq 0 $ ，故 $$ L-H(X) \geq 0 \Rightarrow L \geq H(X) $$
最优码长的界
定理： 设 $l_1,l_2,\cdots ,l_m$ 是关于信源分布 $p$ 和一个二元字母表的一组最优码长，$L$ 为最优码的期望长度 $L = \sum p_il_i$ ，则有 $$ H(X) \leq L < H(X)+1 $$ 证明： 由上面的证明可知下界为 $H(X) \leq L$，下证 $L < H(X)+1$，由于码长 $\log \frac{1}{p_i}$ 不一定为整数，因此我们取 $$ l_i = \lceil \log \frac{1}{p_i} \rceil $$ 则 $$ \log \frac{1}{p_i} \leq l_i<\log \frac{1}{p_i}+1 $$ 左右两边用 $p_i$ 加权得到： $$ H(X) \leq L <H(X)+1 $$
香农码
设随机变量 $X$ 取 $m$ 个值，概率分布为 $p_1,p_2,\cdots,p_m$。按照概率值大小排序为：$p_1»p_2\cdots»p_m $，定义累计函数 $$ F_i = \sum_{k=1}^{i-1}p_k $$ 保留 $F_i$ 的 $l_i$ 比特作为 $i$ 的码字，其中 $l_i = \lceil \log \frac{1}{p_i}\rceil$
例子： 概率分布为 (0.5,0,25,0.125,0.125)
| p | l | F | Bin | Code |
|---|---|---|---|---|
| 0.5 | 1 | 0.000 | 0.000 | 0 |
| 0.25 | 2 | 0.500 | 0.100 | 10 |
| 0.125 | 3 | 0.750 | 0.110 | 110 |
| 0.125 | 3 | 0.875 | 0.111 | 111 |
定理：香农码是前缀码，其构造的编码是无前缀的。
证明： 设 $x_i$ 为 $x_j$ 的前缀，则 $l_i <l_j$ ，即 $$ \lceil \log \frac{1}{p_i} \rceil < \lceil \log \frac{1}{p_j} \rceil \Rightarrow p_i>p_j $$ 则 $F_j>F_i$ ，又 $$ l_i =\lceil \log \frac{1}{p_i} \rceil \Rightarrow \log \frac{1}{p_i} \leq l_i <\log \frac{1}{p_i}+1 \Rightarrow p_i \geq 2^{-l_i} $$ 作差得： $$ \begin{aligned} F_j-F_i =& 0.y_1y_2\dots y_{l_j}\dots -0.y_1y_2 \dots y_{l_i}\dots\\ =&0.00 \dots y_{l_{i+1}} \dots y_{l_j} \dots \\ <& 2^{-l_i} \leq p_i \end{aligned} $$ 而 $$ F_j-F_i = \sum_{p>p_j} p - \sum_{p>p_i} p =p_i+p_{i+1}+\cdots+p_{j-1}>p_i $$ 与上面矛盾，故对 $\forall l_i <l_j$ ，$x_i$ 都不为 $x_j$ 的前缀。
定理（香农码的上下界）： 香农码的上下界满足如下关系 $$ H(X) \leq L <H(X)+1 $$ 证明： 根据香农码的码长 $$ l_i = \lceil \log \frac{1}{p_i} \rceil $$ 得： $$ \log \frac{1}{p_i} \leq l_i<\log \frac{1}{p_i}+1\\ \sum_i p_i \log \frac{1}{p_i} \leq \sum_i p_il_i < \sum_i p_i \log \frac{1}{p_i} +\sum_ip_i\\ H(X) \leq L<H(X)+1 $$
Huffman 编码
将概率最小的两个随机变量合并，然后再进行排序，再将概率最小的两个值进行合并，然后在进行排序，直到合并到 1 为止。
例子：
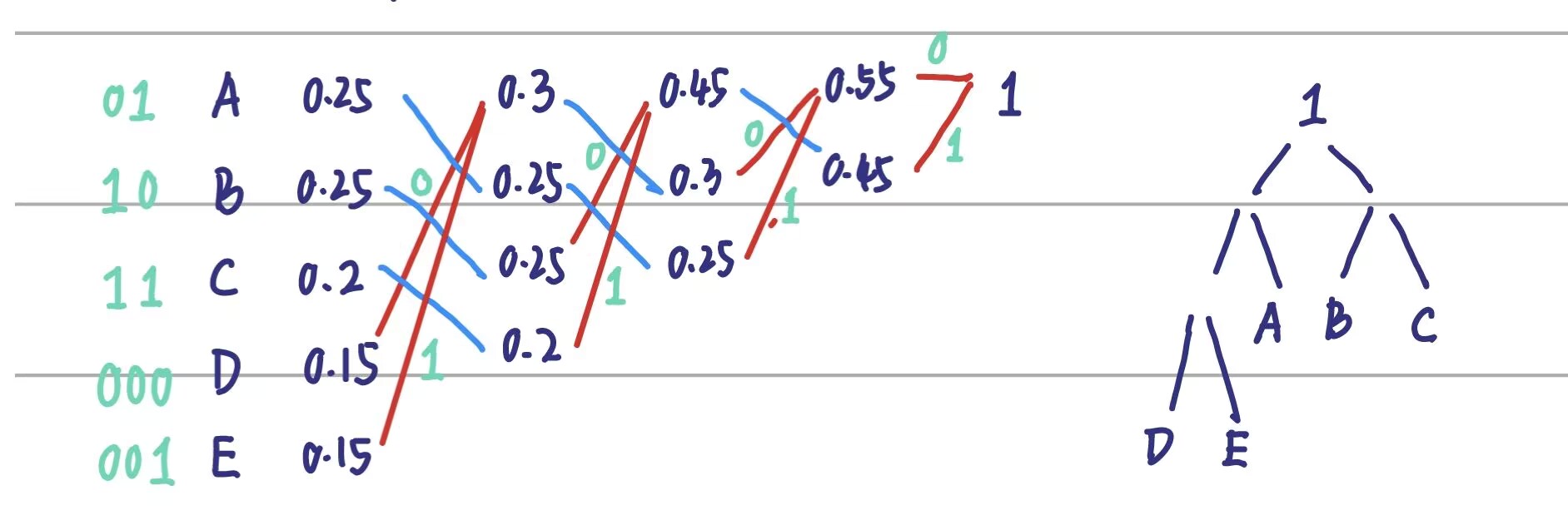
定理：对于任意一个分布，必然存在满足如下性质的一个最优即时码：
-
其长度序列与按概率分布的排列顺序相反，即若 $p_j>p_k$，则 $l_j\leq l_k$。（反证法显然）
-
最长的两个码字具有相同的长度。（必然为同一个节点的两个儿子）
-
最长的两个码字仅在最后一位上有区别，且对应两个最小可能发生的字符。